导读:在一些实际应用中,分布式优化问题的求解需要由连续时间演化的物理系统(智能体)完成,例如协同控制中的无人机和电网经济调度中的发电机系统。然而,现有的基于零梯度和(Zero-gradient-sum, ZGS)算法的分布式优化工作大多聚焦于具有一阶动力学的智能体,并且由这些算法所推导的收敛时间上界表达式复杂,不利于用户自主调节。近日,本研究团队提出了一种基于时变函数的预定义时间零梯度和优化算法,其收敛时间界可通过单一参数进行预调节,为具有受扰二阶动力学系统的分布式优化问题提供了新方案。
一、研究背景与核心挑战
相比于由一阶动力学描述的系统,受扰的二阶动力学形式能更准确地描述实际物理系统的运动行为。ZGS算法因其解决分布式优化问题的独特视角而被广泛研究与应用。因此,将ZGS算法拓展至受扰二阶多智能体系统贴合理论与实际应用需求。
传统的ZGS算法多为渐进收敛或有限时间收敛,难以预先给定到达最优解的收敛时间。其中,部分有限时间收敛算法依赖于系统初始状态,应用场景受限。现有的固定时间ZGS算法虽然摆脱了对系统初始状态的依赖,但其收敛时间界的表达式往往是复杂的,不易于调节。具体而言,ZGS算法的固定时间收敛大多基于类李雅普诺夫函数方法(Lyapunov-like Function Method)。一种常见的实现固定时间收敛的类李雅普诺夫函数方法如下:
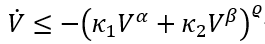
其中k1,k2,α,β,Q>0,且收敛时间界是一个由这些参数组成的复杂分式。因此,分布式优化算法中将不可避免的引入基于状态的分数阶项。针对相对阶为2的受控系统,在滑模控制框架下,上述方法可能会导致优化算法出现奇异性;同时上述不等式条件会被重复使用,这会增加在收敛性分析和控制设计上的复杂度。
二、理论创新
面对上述挑战,本研究引入与状态无关的时变函数,并将其与先进的无局部最小化ZGS算法相结合,在滑模控制框架下,提出如下分布式优化算法:
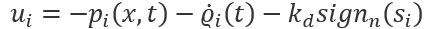
其中,
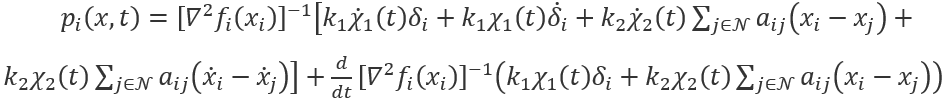
时变函数Qi(t),x1(t),x2(t)的引入保证了智能体状态的预定义时间收敛且避免了所提算法涉及状态的分数阶项,便利了收敛性分析与控制设计。此外,范数归一化符号函数signn(*)替代了传统符号函数sign(*),这有益于抑制输入抖振。
特别地,该算法具有双滑模嵌套结构:
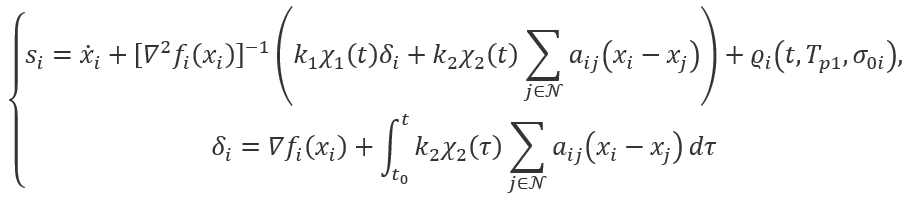
滑动变量si:当si=0时,受扰的二阶系统等效为一阶动力学且该过程在预定义时间内实现,由时变函数Qi(t,Tp1,σoi)保证。
滑动变量δi:在预定义时间内δi=0被保证时,这意味着ZGS流形被建立;随后,在预定义时间内实现分布式优化,即所提算法实现对全局最优解的预定义时间收敛;分别由时变函数x1(t)和x2(t)保证。
三、性能优势:理论保证与仿真验证
滑模控制方法的使用确保了所提算法对输入扰动的强鲁棒性。
状态无关的时变函数的引入确保了所提优化算法的收敛时间界可通过单个参数任意调节,不再要求状态依赖的分数阶项,简便了面向二阶多智能体系统的稳定性分析与控制器设计。
双滑模嵌套结构使得ZGS算法拓展至受扰二阶多智能体系统依然有效。此外,如果δi=0,那么si=0所对应的动力学则是可解决具有一阶动力学的分布式优化问题的预定义时间ZGS算法,即,所提ZGS算法隐含一阶特例。
仿真验证结果如下图所示:
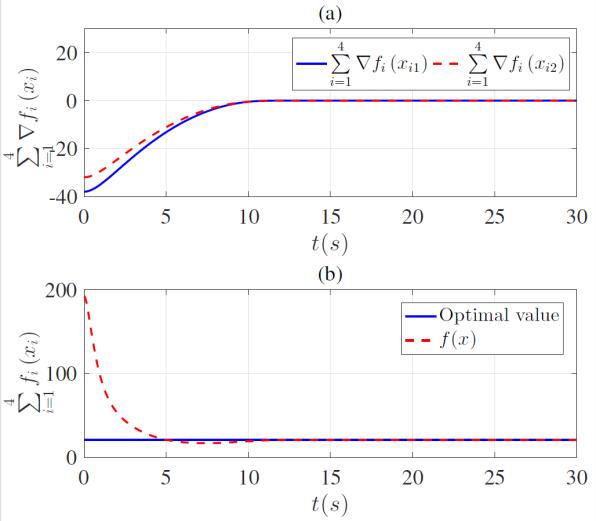
图1:位置xi∈R2,i=1,2,3,4,的3D视角
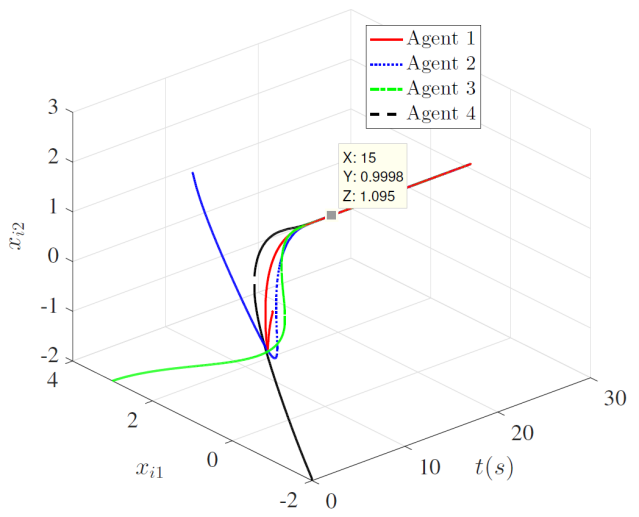
图2:所提算法下代价函数和梯度的变化曲线
四、应用与展望
大多实际物理系统可建模为二阶动力学形式,例如欧拉-拉格朗日系统。因此,本研究提出的ZGS优化算法与它们天然匹配,可直接适用于多种类型的控制对象。收敛时间上界可独立于初始状态进行理论预估并可通过单个参数预先给定,这意味着用户在应用中可按实际需求快速设定优化参数。所提算法具有强鲁棒性,可用于各种有界输入扰动情况。在未来的研究中,如果考虑离散时间通信,比如事件触发,所提优化算法将在收敛性分析与控制设计上提供极大便利性。本研究由大连海事大学博士生江涛、阎妍教授与于双和教授以及东北大学郭戈教授共同完成,阎妍教授为通讯作者。相关工作发表于控制领域TOP期刊《Automatica》。
论文信息:Tao Jiang, Yan Yan, Shuanghe Yu, Ge Guo. “Predefined-time distributed optimization for second-order multiagent systems: Zero-gradient-sum scheme”. Automatica, 185, 112743, 2025.